| Earth curvature calculation spreadsheet | ||||||||
| Labels | Values | formula | ||||||
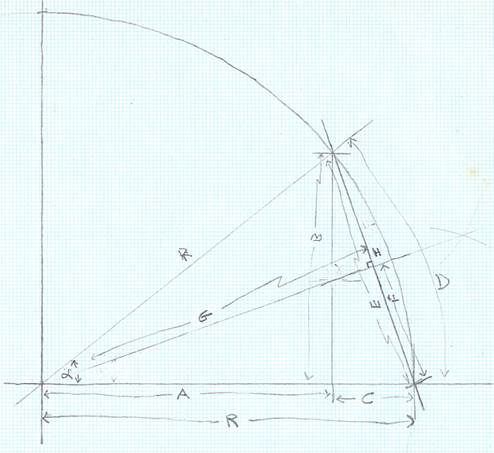
| R, radius of Earth (miles) | 3963 | |||||||
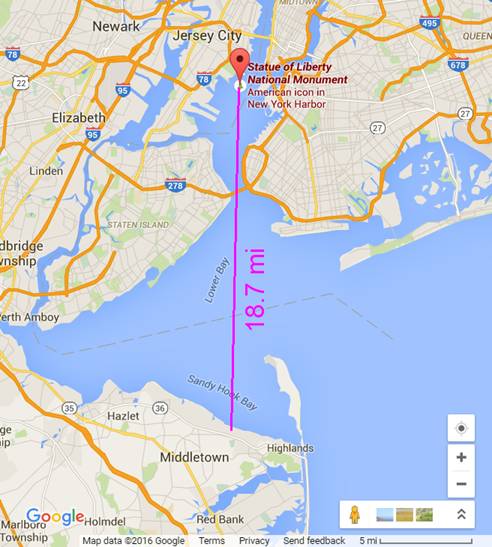
| D, distance from observer (miles) | 18.7 | |||||||
| α, angle to observer (radians) | 0.004718647 | D / R | ||||||
| A | 3962.955881 | R ∙ cos(α) | ||||||
| B | 18.69993061 | R ∙ sin(α) | ||||||
| C | 0.044119272 | R - A | ||||||
| E | 18.69998265 | sqrt(B²+C²) | ||||||
| F | 9.349991326 | E / 2 | ||||||
| G | 3962.98897 | sqrt(R²-F²) | ||||||
| H | 0.011029833 | R - G | ||||||
| H in feet | 58.2375203 | H x 5280 ft/mi | ||||||
| Calculate the height of the effective barrier between observer and object under observation, | ||||||||
| created by the curvature of the Earth, as a function of the distance between observer and | ||||||||
| object under observation. I.e., calculate the maximum height difference between a straight | ||||||||
| line and a curve which follows the curvature of the Earth. | ||||||||

|
||||||||
| The fundamental deficiency in this approach is the assumption that Earth has no atmosphere. | ||||||||
| In the real world, the Earth's atmosphere acts as a lens, which refracts light. Depending | ||||||||
| on atmospheric conditions, it is often possible for things beneath the horizon to appear at the | ||||||||
| horizon, or even above the horizon. Here are a couple of very good web pages on this topic: | ||||||||
| http://aty.sdsu.edu/~aty/explain/atmos_refr/horizon.html | ||||||||
| http://aty.sdsu.edu/~aty/explain/atmos_refr/altitudes.html | ||||||||

|
||||||||
| Note: the previous version of this spreadsheet (using 60 miles as the distance) is here: | ||||||||
| http://www.sealevel.info/Earth_curvature_calculation_spreadsheet_v1.htm | ||||||||
| This is an exported Excel spreadsheet. You can load it directly into | ||||||||
| Microsoft Excel 2003 or later, or another compatible spreadsheet | ||||||||
| program, such as Kingsoft WPS Office "Spreadsheets" (but not | ||||||||
| OpenOffice), to view (or change) the formulae & values. | ||||||||
Dave Burton
30 April, 2016
(minor updates 3 November, 2017)